Introducción
En matemáticas y ciencias de la computación, un grafo es un sistema compuesto por un conjunto de nodos unidos por enlaces llamados arcos. Un grafo permite representar relaciones entre elementos de un conjunto.
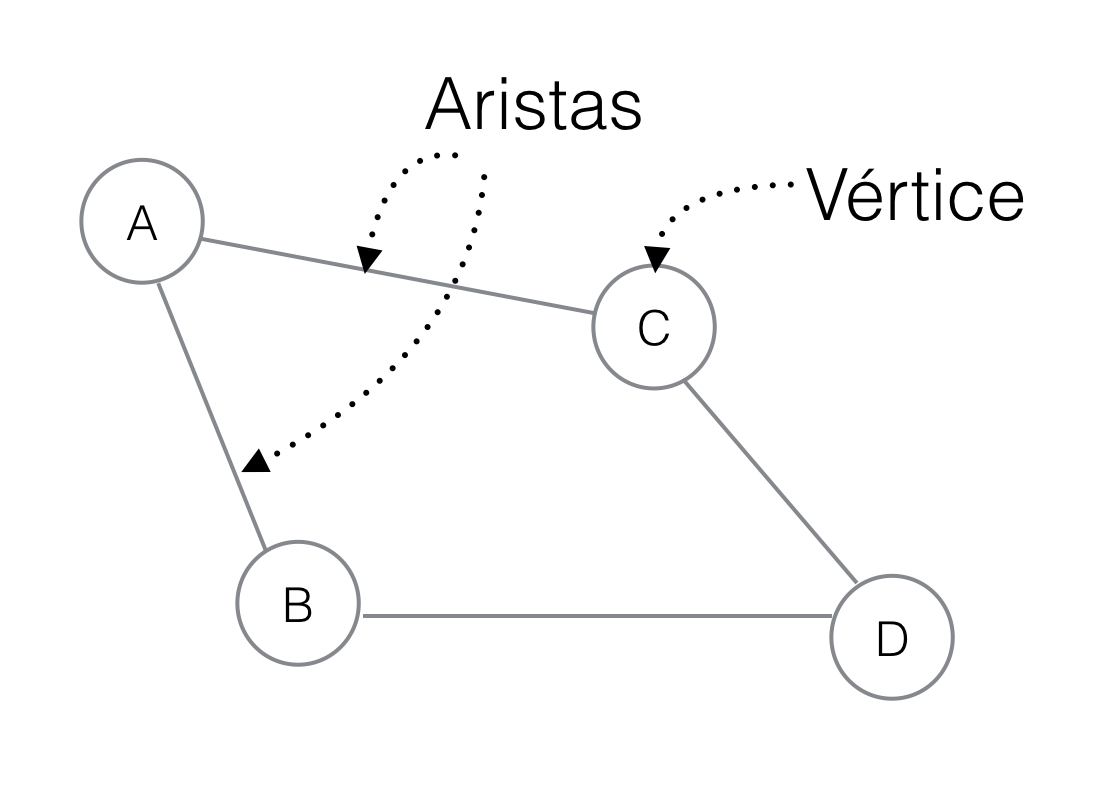
Representación gráfica de un grafo
En informática, el algoritmo Floyd-Warshall es un algoritmo de análisis de grafos, que de forma eficiente y simultanea, encuentra los caminos más cortos entre todos los pares de vértices dentro de un grafo en una única ejecución. El algoritmo Floyd Warshall es un ejemplo de programación dinámica.
Las aristas tienen un valor que puede positivo o negativo, pero para que haya coherencia numérica Floyd-Warsall supone que no hay ciclos negativos. No obstante, si hay ciclos negativos, ya que si los números de la diagonal de la matriz de caminos son negativos es condición necesaria y suficiente para que este vértice pertenezca a un ciclo negativo.
Muchos problemas de la vida cotidiana se pueden expresar e incluso resolver en forma de grafo. El grafo se representa en una tabla(matriz) que se conoce como matriz de adyacencia" y representa si existe una unión entre dos nodos por ejemplo:


Aplicaciones
El algoritmo de Floyd-Warshall puede ser utilizado para resolver los siguientes problemas, entre otros:
*Algoritmo de Floyd.
*Algoritmo de Warshall.
*Algoritmo de Kleene.
*Ruta óptima.
*Algoritmo de Gauss-Jordan.
*Comprobar si un grafo no dirigido es bipartito.
*Calculo rápido de redes de organización de datos.
*Caminos de máximo ancho de banda.
Implementación en Python
class grafico:
def __init__(self):
#Diccionario que contiene las claves que se asignan a los correspondientes objetos vértice
self.vertices={}
def add_vertex(self,key):
#Agrega un vértice con la clave dada al gráfico
vertex=Vertex(key)
self.vertices[key]=vertex
def get_vertex(self,key):
#Devuelve el objeto vértice con la tecla correspondiente
return self.vertices[key]
def __contains__(self,key):
return key in self.vertices
def add_edge(self,src_key,dest_key,weight=1):
#Agrega borde desde src_key hasta dest_key con el peso dado
self.vertices[src_key].add_neighbour(self.vertices[dest_key],weight)
des does_edge_exist(self,src_key,dest_key): #Devuelve True si hay borde de src_key a dest_key
return self.vertices[src_key].does_ot_point_to(self.vertices[dest_key])
def __len__(self):
return len(self.vertices)
def __iter__(self):
return iter(self.vertices.values())
clas Vertex:
def __init__(self,key):
self.key=key
self.points_to={}
def get_key(self):
#Devuelve la tecla correspondiente a este objeto vertice
return self.key
def add_neighbour(self,dest,weight):
#Hacer que este vértice apunte a dest con el peso del borde dado
self.points_to[dest]=weight
def get_neighbours(self):
#Devuelve todos los vértices señalados por este vértice
return self.points_to.keys()
def get_weight(self,dest):
#Obtener peso de borde desde este vértice a dest
return self.points_to[dest]
dest does_it_point_to(self,dest):
#Devuelve True si este vértice apunta a dest
return dest in self.points_to
def floyd_warshall(g):
#Devuelve los diccionarios distance y next_v.
#distance[u][v] es la distancia más corta desde el vertice u a v.
#next_v[u][v] es el vértice siguiente después del vértice v en la ruta más corta desde u hasta v.
#No es igual si no hay ruta entre ellos.
#next_v[u][u] debe ser None (ninguno) para todos los u.
#g es un objeto de gráfico que puede tener pesos de borde negativos
distance={v:dict.fromkeys(g,float('inf'))for v in g}
next_v={v:dict.fromkeys(g,None) for v in g}
for v in g:
for n in v.get_neighbours():
distance[v][n]=v.get_weight(n)
next_v[v][n]=n
for v in g:
distance[v][v]=0
next_v[v][v]=None
for p in g:
for v in g:
for w in g:
if distance[v][w]>distance[v][p]+distance[p][w]:
distance[v][w]=distance[v][p]+distance[p][w]
next_v[v][w]=next_v[v][p]
return distance,next_v
def print_path(next_v,u,v):
#Imprime la ruta más corta desde el vértice u hasta v.
#next_v es un diccionario donde next_v[u][v] es el siguiente vértice despues del vértice u en la ruta más corta desde u hasta v.
#Es None (ninguno) si no hay una ruta entre ellos.
#next_v[u][u] debe ser None para todo u.
#u y v son objetos de Vertex.
p=u
while (next_v[p][v]):
print('{} ->'.format(p.get_key()),end='')
p=next_v[p][v]
print('{}'.format(v.get_key()),end='')
g=grafico()
print('******Option Menu********')
print('add vertex <node>')
print('add border <from> <to> <weight>')
print('floyd-warshall')
print('toshow')
print('exit')
while True:
do=input('what would yo like to do?').split()
operation=do[0]
if operation == 'add':
suboperation = do[1]
if subopetarion=='vertex':
key=int(do[2])
if key not in g:
g.add_vertex(key)
else:
print('the vertex already exists.')
elif suboperation== 'border':
src=int(do[2])
dest=int (do[3])
weight=int(do[4])
if src not in g:
print('vertex {} does not exist.'.format(src))
elif dest not in g:
print('vertex {} does not exist.'.format(dest))
else:
if not g.does_edge_exist(src,dest):
g.add_edge(src,dest,weight)
else:
print('the edge already exists.')
elif operation == 'floyd-warshall':
distance,next_v= floyd_warshall(g)
print('Shorter distances:')
for start in g:
for end in g:
if next_v[start][ende]:
print('from {} to {}:'.format(start.get_key(),end.get_key()),end='')
print_path(next_v,start,end)
print('distance {})'.format(distance[start][end]))
elif operation == 'toshow':
print('vertex: ',end='')
for v in g:
print(v.get_key(),end='')
print()
print('border: ')
for v in g:
for dest in v.get_neighbours():
w=v.get_weight(dest)
print('from={},to={},weight={})'.format(v.get_key(),dest.get_key(),w))
print()
elif operation == 'exit':
break
Utilización del código anterior
Supongamos tener que realizar una conexión cableada entre distintas computadoras ubicadas en un mismo edificio y planta, la cual gráficamente se ve así:
Los nodos 1,2,3,4 y 5 representan a las computadoras.
Los valores entre nodos representan las distancias entre computadoras.
para utilizar el algoritmo escrito en python debemos:
1- Ingresar primero todos los nodos
2- Ingresar nodo origen, nodo destino y distancia
3- Escribir floyd-warshall
*Lo escrito en negro es lo que yo ingreso por teclado
*Una vez ingresado floyd-warshall, me mostrara lo siguiente:
*Podemos observar la distancia mínima entre los distintos nodos.
Por ejemplo si quiero ir de 1 a 5, el algoritmo me muestra:
Gráficamente seria:
Aplicaciones propuestas
1- Una empresa desea saber cual es la ruta más económica en sus recorridos entre ciudades/barrios donde presta el servicio.
2-Una persona quiere saber que recorrido es el mas económico, ya sea para hacer envíos o dejar a sus compañeros en sus casas.
3-Una empresa de transporte desea saber cual es el camino más corto para realizar entrega de lácteos y carnes en distintas ciudades.
4-Una empresa de correo necesita optimizar la entrega de encomiendas o cartas, para ello necesita saber cual es la ruta mas corta entre los diferentes destinos.
SI TE INTERESA DÉJAME TU CORREO ELECTRÓNICO EN LOS COMENTARIOS Y TE ENVÍO EL CÓDIGO👇

Comentarios
Publicar un comentario